Non-binary Inputs

A number of schemes are possible to represent non-binary inputs to a pRAM network.

PULSE STREAMS

Real_valued inputs are converted to spike trains of a given mean firing frequency using non-learning pRAMs.
If one memory location within a pRAM represents the real number and this location is repeatedly addressed, then the output of that pRAM will have a mean firing frequency which approaches the real number, as the spike train length tends to infinity.
With 6-input pRAMs, up to 64 real numbers can be stored as weights. By fixing the input vector of the pRAM, any given weight can be addressed. In this way, up to 64 training patterns can be stored in the hardware of a pRAM network and can quickly be accessed without requiring the pRAM-256 to be halted.


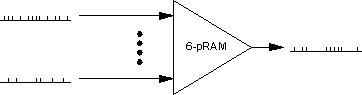
To convert a spike train back to a real number, integrate the output over a period of time.

BINARY INPUTS

An n-bit binary input can be applied in parallel to one pRAM (if n<=6) or to a number of pRAMs.
This method is costly in terms of the number of pRAM inputs it uses.

The use of binary inputs does not convey to a pRAM network the relative significance of the individual bits in the input. The network has to learn this significance during training.
It is better to use thermometer coding, or Grey-coding to represent neighbouring binary vectors since the Hamming distance between input codes offers a better representation than linear binary coding.

With multiple binary input vectors, it is desirable for pRAMs in the input layer to see as many of these vectors as possible to be able to learn the correlations between input vectors.
In such cases, the most significant bits of the input vectors should be taken to the same pRAM, where possible. This pRAM will then learn a coarse mapping of the inputs. Other pRAMs will be used to operate on the less significant bits of the input data.

BINARY INPUTS

An n-bit binary input can be converted to a 6-bit unary coded input as shown.

The non-learning pRAMs below have identical, linearly-increasing weights. These produce six stochastic, unary-coded pulse trains for the main pram.
This produces a form of thermometer coding, if integrated over time.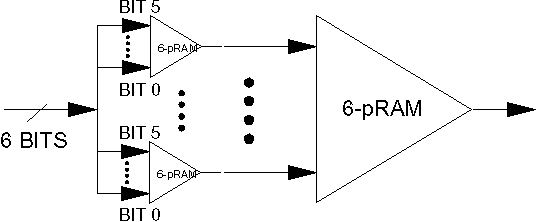
The inputs to the pRAM are a set of pulses whose density is proportional to the input binary number. Therefore the memory locations accessed are related to the magnitude of the input. A cluster of memory locations are accessed over time, due to the stochastic spike trains.

More data

T G Clarkson, August 1995